By Olivier Haillant, David Dumbleton
.jpg)
 The first step in such a testing scenario is to anticipate what the modules will be exposed to in the real world. This has been done with the assistance of large amounts of climatological data obtained for a variety of locations around the world where the products can be expected to be installed. How then, can the thermal exposure anticipated for the PV modules be modeled, duplicated, or in fact, accelerated, given that there are upper thermal destruct limits? The first step in such a testing scenario is to anticipate what the modules will be exposed to in the real world. This has been done with the assistance of large amounts of climatological data obtained for a variety of locations around the world where the products can be expected to be installed. How then, can the thermal exposure anticipated for the PV modules be modeled, duplicated, or in fact, accelerated, given that there are upper thermal destruct limits?
Numerous attempts have been made to develop test protocols that will reveal the aging mechanisms by which PV modules can be expected to fail. However, most of these are HALT/HAST type tests that duplicate or otherwise bring out infant mortality issues, not long term effects. A new approach to obtaining this kind of long term aging data, but in a significantly shorter time frame, is the Atlas 25PLUS program, in which PV modules are subjected to concurrent stresses bounded by levels induced in nature, as pictured in Figure 1.2) To determine the acceleration factors in such a complex test protocol is essentially impossible, but estimates can be made of the increase in chemical degradation incurred by the higher levels of some of the stresses. In this paper, we discuss the acceleration factors that can be induced by changing temperatures and solar irradiance in known ways, using the complex accelerated laboratory weathering step of the Atlas 25PLUS program as example. We seek to demonstrate that at least one part of this reality based test protocol has its basis in theoretically derived factors that can be estimated. Acceleration factors due to the increase in both thermal energy and irradiation, as well as acceleration factors resulting from the increase in temperature for pure thermally activated processes (in the absence of light) are derived.

Acceleration of Temperature Dependent Processes
Acceleration of Pure Thermal Degradation Processes
For temperature dependent processes, the Arrhenius law in Equation 1 may be applied to predict the increase in rate resulting from an increase in temperature, as shown by Equation 2.3)

Where k is the rate constant of the process
A is an Arrhenius pre-exponential factor
Ea is the apparent activation energy
R is the gas constant
T1, T2 are the sample temperatures
AFT is the acceleration factor for thermal degradation (ratio of rate constants)
Acceleration of Photochemically Induced Processes
In presence of light, the rate constant of photochemical processes depends upon both the effective irradiance and the temperature (Equation 3). Equation 4 is used to predict the increase in rate of a process through increasing temperature and irradiance.
where I1 and I2 are the effective irradiances
AFL is the acceleration factor resulting from higher irradiance
AF is the overall acceleration factor

Necessary Assumptions and Approximations
To obtain these equations, several assumptions and approximations are necessary:
-In Equation 1 and 3, the rate constant k applies to a single change in property or performance. For instance, if a material degrades through color change and loss in mechanical properties, both degradation processes will most likely exhibit distinct rate constants.
-The overall temperature dependent process (either in the presence or absence of light) leading to a change in performance follows an Arrhenius dependency
-The rate constant varies linearly with irradiance in the range of irradiances considered. This may not be the case for all polymers or at high irradiances such as several times the maximum daytime irradiance near the equator. In such case, a power law may apply to irradiance.4), 5)
-The activation energy Ea of the overall temperature dependent process (in the presence or absence of light) is constant over the considered temperature range.
-Activation energies for weathering under accelerated conditions are only known for a few materials. When the activation energy of a particular material is not available, it needs to be estimated from published activation energies for similar materials, or determined from in-house experiments. For instance, although the activation energy of the photochemical yellowing of EVA has not been published, it can be estimated from the Ea of the photochemical yellowing established for a range of aromatic polymers.6)
-In Equation 4, the ratio of effective irradiances is approximated to the ratio of total or UV solar irradiances. This approximation is justified when the spectral power distribution of the light sources for test conditions 1 and 2 are very similar.
Limits of the Arrhenius-based Model
As shown above, the Arrhenius equation can be used to quantify the effect of varying temperature and irradiance on the rate of a property change. However it cannot provide a complete picture of the long-term degradation of PV modules, as other stress factors or combination of stresses are involved. These include moisture (inducing physical and chemical processes and generating mechanical stress in combination with temperature), temperature cycling (generating thermomechanical stress), electricity production (inducing electrical and electrochemical stresses), and other externally applied stresses (wind, hail, airborne pollutants, marine air, air blown sand...).
The Issue of Outdoor Variability
Assuming that the values of T1, T2, I1, I2 and Ea are known, acceleration of test conditions 1 vs. test conditions 2 (k1/k2 or AF) can be estimated from Equation 4.
An issue arises when any test condition refers to an outdoor environment, where temperature and irradiance continuously vary, as illustrated in Figure 2 for two outdoor locations. How can these variations be accounted for in Equation 4, which requires a defined value for each input parameter? In other words, what is a relevant value for temperature and irradiance outdoors?
For I2, since k is assumed proportional to the irradiance from Equation 3, it is justified to use the arithmetic mean of the irradiance over the considered period. For the data shown in Figure 2, the mean total solar irradiances in Miami and in Phoenix respectively are 247 W/m2 and 302 W/m2.
The same does not apply to T2, due to the exponential dependence of k with temperature. To overcome this issue, it was suggested that there should be a constant effective temperature Teff which produces the same amount of photodegradation as the naturally varying temperature after exposure to the same amount of sunlight.7) Similarly, there should be an equivalent temperature Teq that would produce the same amount of thermal degradation (in the absence of light) as a varying temperature for the same time.8) The next section details how effective temperatures and equivalent temperatures are determined.
Analytic Expression of Effective and Equivalent Temperatures
It is established that the damage D caused by the combination of light and heat over a period of time can be described by Equation 5.9), 10)

where It and Tt are the effective irradiance and material temperature respectively at time t
¡ât is the time interval for the observations
By substituting Tt by a constant effective temperature Teff which would result in the same amount of damage as induced by the naturally varying temperature after exposure to the same amount of sunlight, Equation 6 is obtained.

Setting Equation 5 and 6 equal to each other and rearranging gives Equation 7.

The physical meaning of Teff is the irradiance-weighted average temperature for a data set. One year¡¯s worth of irradiation applied at Teff should give the same degradation as one year¡¯s worth of irradiation applied at the naturally varying light intensity and temperature assuming a cumulative damage model.
For pure thermal degradation processes, Equation 8 is used, obtained through removing It from both terms of Equation 7. Again, this requires a value of Teq, which represents the amount of degradation that would have occurred at a constant temperature in the absence of solar radiation.

To access Teff and Teq, detailed radiation and temperature data related to the exposed material/product/system must be available, for instance 10-minute parsed.
Application to the Determination of Acceleration Factors
Objective
Polymeric materials used in the composition of PV modules accumulate degradation from exposure to UV radiation, temperature excursions, moisture, and mechanical loads. The analysis below focuses on all photochemically induced processes that contribute to the loss of performance of PV modules, such as embrittlement, delamination and/or discoloration. Results of calculation done for pure thermally driven processes are also given.
Two sets of effective temperature Teff and equivalent temperature Teq will be calculated in the context of the Atlas 25PLUS Program, for the two reference outdoor locations and for the laboratory test, both types of conditions having varying parameters. The acceleration factors will then be determined.

 The Atlas 25PLUS Program The Atlas 25PLUS Program
The core element of Atlas 25PLUS is an accelerated laboratory weathering sequence in which the following tests occur:
a) exposure to 120 cycles of AM 1.5G solar radiation, temperature and humidity (STH) at nature-derived levels for seven days of each ten day sequence
b) exposure to 40 cycles of AM 1.5G solar radiation, temperature and humidity under freeze/thaw conditions (STHF) typical of temperate climates for the other three days
In the standard version of the program, the sequence a) + b) is repeated 8 times, totaling 960 STH and 320 STHF cycles. The average total irradiance is 559 W/m2.
Because of the cyclic nature of this sequence, effective temperatures and equivalent temperatures will be calculated to estimate the acceleration obtained over reference outdoor exposures.
Reference Outdoor Locations
In this example, the reference outdoor locations are the Atlas benchmark exposure sites DSET Laboratories in Phoenix (hot arid climate) and SFTS in Miami (hot humid/subtropical climate) for which detailed temperature and solar radiation data are available. As there is no temperature data available for real modules tested against Atlas 25PLUS, the temperature data of a BPT exposed at 5¡Æ facing south will be used instead, which is believed to approximate fairly well the temperature measured at the back of PV modules. When such temperature data is not available, models can be used to calculate the temperature of modules using ambient temperature, solar irradiance and wind speed data.11)
Activation Energies
Activation energies for photochemically and thermally driven degradation processes of PV modules are very material, design and construction dependent and would need to be determined for each type of PV construction from a rigorous experimental design. Furthermore, published activation energy data for the photochemical degradation of polymers are very scarce.6), 12) For our purpose, activation energy values of 60 kJ/mol and 100 kJ/mol were assumed, in accordance with published data for the thermal degradation processes causing performance losses in PV modules.8)

Determination of Teff and Teq for Reference Outdoor Locations
Table 1 shows a small portion of 10-min parsed temperature data (column C) and irradiance data for the total solar radiation spectral range (column D) for Phoenix in 2007 tabulated in an ExcelTM spreadsheet. A column (E) with the left side of Equation 7 is created. The equation in cell E4 is D4*600/1E6 to convert irradiance in W/m2 into radiant exposure in MJ/m2. Cells E4 to E20 are summed to find the total radiant exposure (cell E2).
A column (F) with the right term of Equation 7 is created. The equation in cell F4 is $D4*600/1000000*EXP(($B$1* 1000/8.314)* (1/(273+F$1)-1/(273+C4))). It takes the activation energy value in cell B1, converts it to J/mol, an
d divides by the gas constant. The assumed effective temperature in cell F1 and the measured temperature in cell C4 are converted from Celsius to Kelvin. An exponential function is applied to the combined term and then multiplied by the irradiance within this time interval (10 min, i.e. 600 s). This is all summed in cell F2. The goal is to adjust Teff so that the sum of the right term (F2) equals the sum of the left term (E2) of Equation 7. A similar process was used to calculate the equivalent temperature for ¡®dark¡¯ thermal processes for the period shown in Table 1 (cell I1), using Equation 8. In that case, the irradiance term is not included in cells I4 to I20 and the sum in H2 is replaced by the number of intervals, since each interval has the same duration.
Table 2 shows the calculated yearly values of Teff and Teq at DSET and SFTS in 2007. It is interesting to note that when UV solar irradiance data were used to calculate Teff, nearly identical values (+/-0.1¡ÆC) were obtained.
Determination of Teff and Teq for the Core Test of Atlas 25PLUS
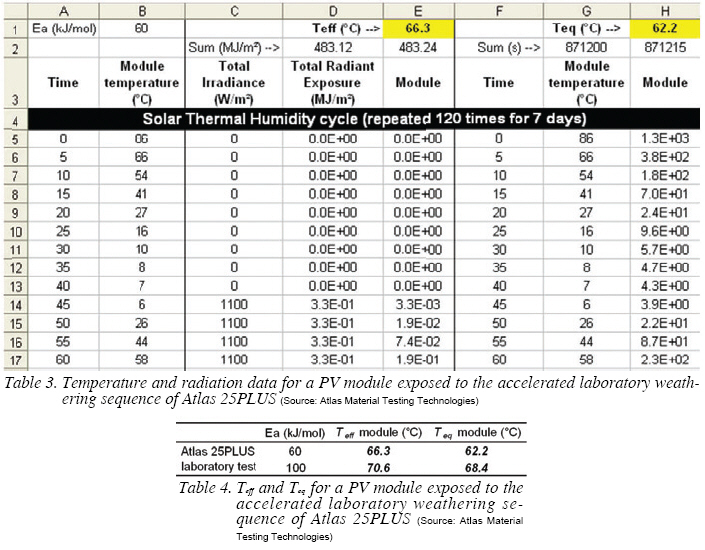
Table 3 shows the temperature and irradiance parameters for a portion of the STH cycle. Column B indicates the temperature measured at the back of a PV module. After 120 STH cycles (or 7 days), 40 STHF cycles are run over 3 days.
The value in cell D5 is the radiant exposure, obtained by multiplying C5 by the time interval between C5 and C6 in seconds and divided by 1E6 to convert W/m2 into MJ/m2. The equation in cell E5 is $D5*EXP(($B$1*1000/8.314)*(1/(273+E$1)-1/(273+B5))). The values of cells D5 to D44 and E5 to E44 are summed in respectively cells D2 and E2, weighing in the ratio of STH/STHF cycles (120/40). The value of Teff in E1 is adjusted so that the value of cell E2 equates that of D2.
The same procedure was used to determine Teq in cell H1, by removing the irradiance term from cells in column H. G2 is the duration of 120 STH + 40 STHF cycles in seconds. The calculated values of Teff and Teq are reported in Table 4.
Determination of Acceleration Factor of Atlas 25PLUS Core Test vs. Outdoors
The values of T1 for Atlas 25PLUS (accelerated laboratory weathering) and T2 for either Phoenix or Miami (outdoor exposures) are reported in the row Teff module (¡ÆC) of Table 5 and Teq module (¡ÆC) of Table 6. The values of I1 and I2 are reported in the row Average irradiance (W/m2) of Table 5. AFT and, in Table 5 only AFL are then determined and multiplied to obtain AF. The correct interpretation of this data is that, for instance, an acceleration factor of 38-40, obtained in the case of Atlas 25PLUS vs. Miami for Ea = 100 kJ/mol indicates that 80 days of the accelerated weathering sequence is expected to produce the same amount of photochemically induced degradation as after 8.5 average years (3,120 days) in Phoenix, assuming that the value of Teff determined for 2007 is representative of an average year.

By segregating out the acceleration effects caused by radiation and thermal increases from those due to thermo-mechanical and humidity effects from cycling, we have shown that a theoretical acceleration factor can be obtained. Although it is highly dependent upon the activation energy Ea, this acceleration factor played a significant role in the development of the Atlas 25PLUS program. By combining these theoretical concepts with several factors from our long term experience in weathering of many different types of products, confidence in the effectiveness of the program was built.
Using an assumed Ea = 100 kJ/mol is not unrealistic. If even one degradation factor has such an activation energy, then the effect will be observed. With this as an assumption, when applied to the 80 day primary weathering cycle of the test, we emerge with an equivalent of almost ten years of equivalent damage in the course of this only three month exposure.
Note that there is likely to be very substantial additional acceleration as a result of the thermo-mechanical stress from the faster thermal cycling. However, it is not currently possible to determine the amount of this increase. Moisture activity in the three phases that are introduced during the test will also have a substantial accelerating effect. Finally, as it has been described in several cases of laboratory and natural weathering, synergistic effects between solar radiation, temperature and humidity (the overall effect is greater than the sum of the individual effects) can be expected. The results of all these accelerations, when taken together, provide a long term environmental durability test unsurpassed in the current venue of photovoltaic evaluations.
Olivier received a Ph.D. in Chemistry (Photochemistry) from the University of Clermont-Ferrand, France. He is currently a senior consultant with Atlas Material Testing (www. atlas-mts.com), and has been with the company since 2005. His current responsibilities include the Solar Competence Center.
David has degrees in Chemistry, Engineering, Physics and a Ph.D. in the micromechanics of polymeric materials. He has worked for a number of companies in R&D roles, most recently as Director of R&D with Alcoa. He is currently a senior consultant with Atlas Material Testing, where he has been since 2006.
REFERENCES
1) O. Haillant, Sol. Energy Mater. Sol. Cells (2010), doi:10.1016/j.solmat. 2010.08.033
2) D. Dumbleton, Photovoltaics World, September/October 2010, p. 22-26
3) R.L. Feller, Accelerated Aging : Photochemical and Thermal Aspects, D. Berland (Ed.), ISBN 0-89236-125-5 (1994), p. 144
4) G. Jorgensen et al, in: J.W. Martin, D.R. Bauer (Eds.) Service life prediction methodology and metrologies. ACS Symposium Series 805, p. 115 (2002)
5) J.E. Pickett et al, Polym. Degrad. Stab., 93 (2008) 1597-1606
6) J.E. Pickett et al, Polym. Degrad. Stab., 93 (2008) 684-691
7) J.E. Pickett, J.R. Sargent, Polym Degrad Stab, 94 (2009) 189-195
8) Kurtz et al, Proceedings of the 34th IEEE Photovoltaic Specialists Conference Philadelphia, Pennsylvania, June 7-12, 2009
8) Bauer D.R., in: J.W. Martin, R.A. Ryntz, R.A. Dickie (Eds) Service life prediction - Challenging the status quo. Federation of Societies for Coatings Technology, p. 39-52 (2005)
10) W.Q. Meeker, L.A. Escobar, V. Chan, in: J.W. Martin, D.R. Bauer (Eds) Service life prediction methodology and metrologies. ACS Symposium Series 805, p. 396-413 (2002)
11) See for instance a) Alonso Garcia et al, Renewable Energy 29 (2004) 1997-2010; b) Mohring et al, Proceedings of the 19th European Photovoltaic Solar Energy Conference, Paris, 7-11 June 2004, p. 2098-2101; c) Amy de la Breteque, Solar Energy 83 (2009) 1425-1433; Mei et al, Solar Energy 83 (2009) 1893-1901; d) Trinuruk et al, Renewable Energy 34 (2009) 2515-2523; e) Ref [8]
12) Cruz-Pinto et al, Angew. Makromol. Chem., 216 (1994) 113-133
For more information, please send your e-mails to pved@infothe.com.
¨Ï2010 www.interpv.net All rights reserved. |